Digital Filters

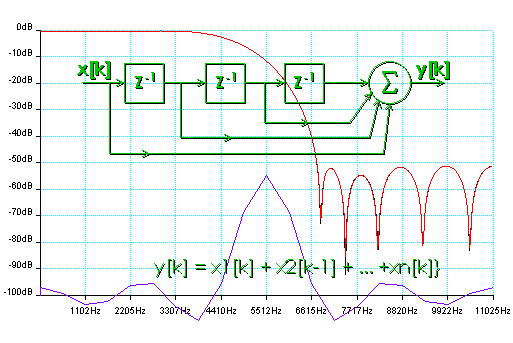
History

This page was originally put together in 1997. Things have moved on since then, particularly in the speed and signal processing capabilities of mainstream processor chips.

However, this code may still be of use. Unfortunately the source code I have - originally written on Borland TurboC++ - will not compile on MS Visual C++ 4.2, and the Borland code doesn't work properly on Windows 2000

Since I can't currently recreate the full executable, the only extant copy is this restricted version. It has the full filter generation code, but it is limited in the length and type of audio files it will filter itself.

To be honest, these days you wouldn't use this program to filter audio - get a professional audio package. It will be faster, and it will probably be able to use plug-ins to open all sorts of files I'd never heard of when this was written. Use the Filter.exe program to generate the filter coefficients.

So, I'm releasing this now as freeware, in the hope that someone will find it useful.

Why this page?

The simple answer is: because I couldn't find this information anywhere else. Every time I picked up a reference on the subject, it was full of poles and zeros, not sensible frequency responses in Hertz and dBs. Most of these references also made my head hurt - it complains when it sees six pages of calculus followed by the phrase 'from this it is obvious...'

The was also a problem in that there seemed to be at least half a dozen ways of working out what went into the filter, with no great preference as to which should be used in a given circumstance - and some of them were much more complicated than others. This wasn't helped by the fact that different references seemed to use different notations and methods...all very confusing!

So, I sat down and wrote some code to design digital filters. Then, I had to write some more code to test the filters with. After that, it made sense to write some more code to implement the filters I'd designed...and so it goes.

Legal stuff

Sorry, but I have to have this in here somewhere.

Basically, you use the information presented on these pages at your own risk.

If anything bad happens because you use this information or software, or you have a bad day, or your dog bites you, sorry, but IT'S NOT MY FAULT.

All software presented here with source code is provided under the LGPL licensing terms. If I don't have the source code any longer, then you are at liberty to use the executables as you wish; with the sole requirement that you acknowledge my original authorship in your source code and documentation.

Thank you.

Filter.exe

Filter will run on any standard PC running Windows 3.1 or Windows95. To generate the filters and to filter an existing .WAV file, the minimum system requirements are a 386 processor and 4Mbyte of memory. Less than half a megabyte of hard disc space is required.

If you wish to use the 'listen' facilities then you will also require a Windows compatible sound card. To listen at the highest rate (44.1ks/s, stereo) you'll need a 486DX2 at 66MHz or better. However, this is not required if you simply wish to generate filter coefficients.

Installation:

Filter is supplied as an executable file (filter.exe), a Borland DLL file (bwcc.dll) and this document (manual.doc). bwcc.dll should be placed in the \windows or \windows\system directories if you do not already have a copy on your system - if you have, ignore it. The manual.doc file is for reference only and you can also ignore this file. Filter.exe may be placed in the directory of your choice - you'll also probably want to make a shortcut to it.

The File Menu:

(Although the illustrations are taken from a Windows 95 environment, the comments apply equally to Windows 2000. It hasn't been tested with Windows XP but there should be no problems.)

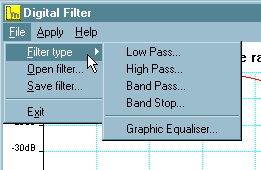The main choices in the filter program are selected from the File menu. Filter Type offers a sub-menu (which can also be quickly accessed using a right mouse click) allowing you to select the type of filter you require. Graphic Equaliser is separated from the rest as it is operated in a slightly different way.

Low Pass and High Pass options are effectively inverses of each other, and therefore offer similar parameter choices.

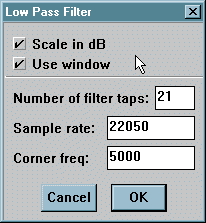
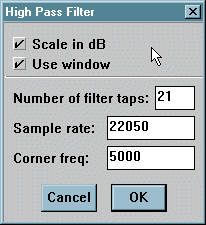
The Scale in dB checkbox controls the way in which the computed frequency response is shown. The default option is to display using a logarithmic (dB) vertical scale: un-checking it lets you see the response in linear form.

Use window is the other default - it applies a Hamming window to the filter to improve both the in-band ripple response and the out-of-band rejection ratio.

Number of filter taps allows you to select the number of coefficients used to create the filter. It is always odd, and can be set between three and four hundred and ninety nine. Generally you will want to keep the number of taps as low as possible (while the filter still meets your specification) to increase the speed of the final filter.

Sample rate is er... the sampling rate! The sampling rate and corner frequencies scale with each other (so the same filter is generated for a 22050 sample rate and 5000 corner frequency, and a 44100 sample rate and 10000 corner frequency) but it is convenient to be able to define the exact frequencies you will be using and not have to bother with the scaling.

Corner frequency defines the point at which the frequency response drops to -6dB relative to the maximum pass band response. Note that the responses are always scaled to show 0dB as the pass band maximum.

Band Pass and Band Stop are again logical inverses of each other. The only difference is that instead of a corner frequency, you have instead a centre frequency to mark the centre of the pass (or stop) band, and a Width entry which sets the gap between the -6dB points.

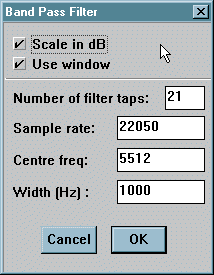
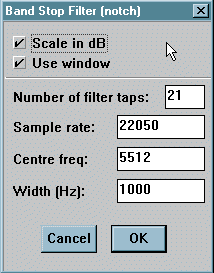
As an example, in the examples shown above, the -6DB points are at 5012Hz and 6012Hz.

The Graphic Equaliser is operated in a slightly different way from the preceding options.

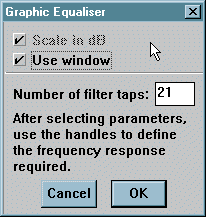
All the other options have no user input once the parameters have been set, but this selection requires you to define the frequency response you require. The only parameters you can change at this point are whether or not you use a window, and the number of filter coefficients. The scaling of the display is automatically returned to logarithmic (dB).

After the 'OK' button is pressed, you are presented with a flat response curve:

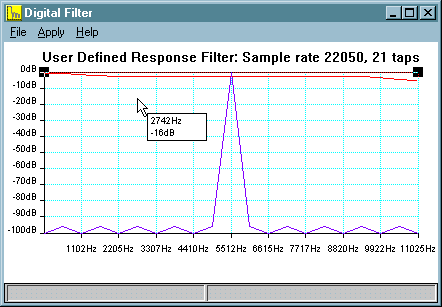
The straight line is the response which the filter will try to track. The black squares are handles which you can use to move the line - left click on a handle and drag to a new position. When the left button is released the filter response is re-calculated. To add another handle, left click on the line. You'll notice that the cursor tracks the frequency and the level as you move. After you've defined a few points you'll see that the program has begun to track the response. The more filter taps you select, the better the tracking will be. You can have a maximum of twenty one handles.

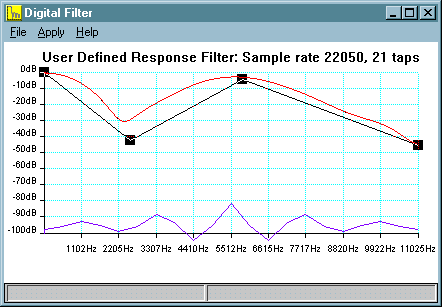
If you need to remove a handle, right click on the handle and you'll be offered a sub-menu with a choice: either remove the handle on which you've clicked, or remove all the handles and restore to a flat response.

The other options offered by the File menu are Open Filter and Save Filter. These allow you to save and load named filters. Because this is a sixteen bit application, the normal 8.3 file names apply, rather than the long filenames available in Windows 95 and later.

Two files are saved: one with an '.inc' extension which can be used as a C++ include file (and which is loaded back into the program on an Open Filter), and a simpler binary file which can be used directly as data by a program. This is a sample of the '.inc' file:

When you include the file, two variables become visible: the defined xxTaps, and a static array xxCoeffs[], where xx is the name of the file (always in capitals). The array contains the 16 bit signed values of the coefficients, with the decimal fractions commented. Note that the commented parts are used by Filter when a file is loaded.

A second file is also saved, this time with the file type '.fir'. Here, the format is simpler: it is a binary file intended to be read by a program (say as a command line parameter). It consists of sixteen bit integer values, the first one being the number of coefficients and the remainder the coefficients themselves. The integers follow normal Intel format, low byte first.

The Apply Menu:

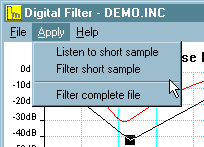Three options are available here. If you have a standard Windows compatible soundcard, then you can use the Listen to short sample to check the first five seconds of a '.wav' file, before you filter it. You can also use Filter short sample to listen to the same sample, but filtered - this action is just a check; it does not make any changes to your file.

Whether you have a soundcard fitted or not, you can still filter a complete file. Be warned: this can take a long time, particularly on a 44.1 ks/s stereo signal, or if you have a filter with a lot of taps. The input '.wav' file must be sixteen bits, but can be both mono or stereo (with the registered version). The input file is not changed as a result of the filtering - a file named 'filtrout.wav' is created which you will need to rename later.

Dos Utilities

Here are a couple of utilities I knocked together some time ago - they're sixteen bit DOS apps built under Borland C++v3.0, though they will run quite happily under Windows 3.1 and later.

Both programs are supplied with both an executable and the source code.

What does Steptone do?

Steptone.exe is a dos executable which creates a test signal suitable for checking the response of digital filters. This output is presently in the form of a Windows 'wave' file, mono, at 22050 samples per second. If you want to change this, you'll have to recompile the code.

The program requires one parameter on the command line, the name of the file you want to create. Full pathnames are supported in the dos 8.3 format. The program will work from the windows 'run' menu option.

The audio content in the file consists of ten groups of tones, each separated by a 0.2s silence. These silences show up on a wave editor's display, and let you see what frequencies still exist after your filter has been at the test file.

Each of the groups of frequencies is further split into 250Hz blocks: i.e. the first block consists of 1000,1250,1500, and 1750Hz. The next group starts with 2000Hz, the third with 3000Hz. The last block is 10000-10750Hz, almost the Nyquist frequency. The entire test burst totals ten seconds. The output is at digital zero level.

Warning: Digital zero level is the absolute maximum level a digital signal can have. Industry technique is to use -18dB as a zero level to leave headroom for high level peaks. You may want to us a product like Cool Edit Pro to reduce the level by at least 3dB before you try any filtering on it as any gain in the filter will produce nasty overload clipping.

How do I use Steptone?

Either at the dos prompt (c:>) or in the windows 'run' box, type 'steptone xxx.wav', where xxx is the name you want for your file output. You must type the .wav bit, or you'll get a correctly built file that you'll have to rename later if you want a windows editor to see it. The program runs in less than a second on a 133 Pentium.

How do I compile Steptone.cpp?

The only thing to remember is that it should be compiled in the LARGE sixteen bit memory model. The original was compiled using Borland Turbo C++ v3.0, but apart from // comments, there are no C++ structures used, so any C or C++ compiler should work without too much fiddling. Use of a 32bit compiler will require attention to the data structures in the very rough and ready wave header code - the variables will all be the wrong size.

What does Fir do?

Fir.exe is a dos executable which performs an FIR filter on a windows 'wave' file. The parameters for the filter can be either defined at compile time, or defined at runtime in an external binary file. Presently, the filter only operates on mono sources at sixteen bits per sample. The sample rate is not important, other than to note that the filter coefficients are calculated as fractional parts of the sample rate. This means that the coefficients which give a 5kHz cutoff on a 22050 sample per second source will give a 10kHz cutoff if the sample rate is 44100.

How do I use Fir?

Either at the dos prompt (c:>) or in the windows 'run' box, type 'fir xxx.wav yyy.wav zzz.fir' where

'xxx' is the name of the file you wish to filter,
'yyy' is the name of the output file,
'zzz' is the name of the filter parameter file.

Note that you must include the extensions ('wav' and 'fir') to use windows wave files. The zzz.fir file can be generated using the program Filter.exe, above. See the notes on using Filter.exe for details of the .fir file format.

How do I compile Fir.cpp?

The only thing to remember is that it should be compiled in the LARGE sixteen bit memory model. The original was compiled using Borland Turbo C++ v3.0, but apart from // comments, there are no C++ structures used, so any C or C++ compiler should work without too much fiddling. Use of a 32bit compiler will require attention to the data structures in the very rough and ready wave header code - the variables will all be the wrong size.

Copyright © 1995-2005 Neil Barnes - 4 April 2005